Ejercicios de cálculos resueltos
Por ejemplo vamos a resolver:
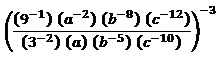
en primera instancia:
((32*b5*c10)/(9*a*a2*b8*c12))-3
luego
(9/(9*a3*b3*c2))-3
es por ello que:
(1/(a3*b3*c2))-3
siendo el resultado final:
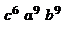
Por ejemplo vamos a resolver:
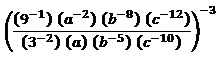
en primera instancia:
((32*b5*c10)/(9*a*a2*b8*c12))-3
luego
(9/(9*a3*b3*c2))-3
es por ello que:
(1/(a3*b3*c2))-3
siendo el resultado final:
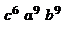
Encontre esta presentación, que luce bien interesante.
He encontrado este interesante artículo siguiendo esta búsqueda en google, https://www.google.co.ve/search?um=1&hl=es&safe=off&rlz=1C2SAVG_enVE521VE521&bav=on.2,or.r_gc.r_pw.r_cp.r_qf.&bvm=bv.41867550,d.dmQ&biw=1280&bih=737&q=%C3%93scar%20Pacheco%20R%C3%ADos%20&ie=UTF-8&sa=N&tab=iw&ei=dPAOUe34O5Se9QTM-4GYAQ
Autor: Oscar Pacheco Ríos
Título del trabajo: ETHNOGEOMETRIA
Tipo de trabajo: Taller
Palabras clave de la temática: Teoría Etnomatemática
"Primero Ethnogeometría para seguir con Etnomatemática"
INTRODUCCION
En esta última década la Etnomatemática se ha presentado, como una nueva corriente del saber matemático, intentando rescatar los valores que el pueblo y su cultura tienen. Esta corriente es vista por algunos con cierto escepticismo y por otros como la nueva alternativa para el aprendizaje de la Matemática. Después de leer a los más prominentes impulsores hemos llegado al convencimiento de que tienen razón, pero, nosotros consideramos que antes que la propia Etnomatemática esta la Ethnogeometría como la antesala de la primera..
I¿QUÉ ES ETNOMATEMÁTICA?
En el intento de situarnos con el tema mismo de lo que trata la Ethnogeometría, consideramos que debemos ver, qué es Etnomatemática. Aunque hay una lista larga de autores que intentan dar una definición exacta, lo haremos según lo señala el Prof. D’Ambrosio, por ser de los precursores más activos y consecuentes y según el resumen analítico del Prof. neozelandés Bill Barton[1].
“Las diferentes formas de matemática que son propias de los grupos culturales, las llamamos de Etnomatemática”[2]
Este es un juicio a fortriori, o actual, pues, los grupos culturales existen y se encuentran por toda la faz de la Tierra. Luego todos los MODOS de MATEMATIZACIÓN que realicen esos grupos culturales para solucionar sus problemas cotidianos, se las puede denominar de ETNOMATEMATICA.
“La ETNOMATEMATICA en mi concepción es etno+matema+tica, eso es, LAS ARTES, TECNICAS, MANERAS, ESTILOS [=TICAS] de EXPLICAR, ENSEÑAR, COMPRENDER, MANEJAR, LIDIAR, "To cope with", "se débrouiller" [=MATEMA] en SU ENTORNO NATURAL y CULTURAL [=ETNO]” Ubiratan D'Ambrosio.[3]
Según esta explicación, “ETNO” es el “ENTORNO NATURAL y CULTURAL” del hombre en una forma atemporal, es decir, no se refiere al hombre primitivo en su condición de cazador o recolector, se refiere al hombre de todas las épocas hasta llegar a la actual, en su diario accionar en su contexto circundante y circunstancial.
Si, “MATEMA” está homologada con “LAS ARTES, TECNICAS, MANERAS, ESTILOS “To cope with" (para cubrir con o abarcar), sí débrouiller” (manejar o dirigir). Significa que es importante referirse, a todas las formas de expresión o exultación mental y espiritual hechas realidad, abarcando de un modo poético, gráfico, pictórico, petroglífico o folklórico con sus propias modalidades.
“TICAS” es una referencia clara a la metodología, es el cómo trasmitir o compartir, cualquier experiencia (inclusive el MATEMA), con otra(s) persona(s) para que esa(s) persona(s) tenga(n) acceso a un nuevo conocimiento. En el entendido que ese nuevo conocimiento le permitirá solucionar sus tribulaciones o le causará el placer de lograr sus metas, pese a los factores socio-culturales que puedan influenciarlo positiva o negativamente.
El mismo creador del concepto antes interpretado y según Eduardo Sebastiani Ferreira dirá que la Matemática es una parte de la Etnomatemática colocada así:
EDUCACIÓN ETNOMATEMÁTICA MATEMÁTICA
donde, dentro de la Educación, “la Matemática se constituiría en una parte de la Etnomatemática”, por tanto para aprender Matemática invariablemente se debe pasar por Etnomatemática.
Al parecer Bill Barton, se preocupa más con esto último y él, después de estudiar a los autores citados en su trabajo, aunque observa que D’Ambrosio se ubica más en la dimensión socio-antropológica, considera que son cuatro, los términos críticos para la definición: Matemática, Matemático, Nosotros y Cultura.
"La Matemática son los conceptos y las prácticas en el trabajo de esa gente quiénes se llaman a sí mismos matemáticos."
"El Matemático se refiere a esos conceptos y a las prácticas, que se identifican como si estuvieran relacionadas en alguna manera a la Matemática".
“ El matemático y la Matemática ambos son culturalmente específicos porque sus referentes dependen de quiénes usan los términos. Es posible, que por ejemplo, que algunos matemáticos disientan sobre lo qué es legítimamente Matemática.”
“En el "nosotros", usamos la definición como un grupo, quienes comparten una comprensión de Matemática y quienes están interesados en Etnomatemática. Que el grupo incluirá comúnmente matemáticos, quienes toman su propia definición, pero incluirán también a otros, quienes han experimentado Matemática como una categoría en su educación propia. Cuando una Cultura étnica diferente, anda implicada con el "nosotros", nos referimos a los miembros de una cultura, que contiene la categoría de matemáticos. El uso puntual del pronombre hace que el etnomatemático tenga un punto de vista particular”
“Cultura se toma para tener el significado usado por D'Ambrosio, que se refiere al grupo de gente quien "desarrolló prácticas, conocimiento, y, en particular, jergas y códigos, que claramente comprende la manera como ellos matematizan, es decir: es la manera que ellos cuentan, miden, relacionan y clasifican, e infieren" (D'Ambrosio 1984). Tal grupo puede ser un grupo étnico, un grupo nacional, un grupo histórico, o un grupo social dentro de una cultura más amplia. La Cultura refiere al conjunto compartido identificable de comunicaciones, comprensión y prácticas. No es necesaria la definición de Etnomatemática si el conjunto es descriptible con exactitud.”
Habiendo definido los términos, hay cuatro de implicaciones de la definición:
a) Etnomatemática no es un estudio matemático; es más como la antropología o historia;
b)La definición en sí misma depende de quien lo afirma, y culturalmente es específico;
c) La práctica que describe es también culturalmente específica;
d)Etnomatemática implica alguna forma de relativismo para la Matemática”.
Analizar estas cuatro implicaciones, equivaldría a elaborar un tratamiento específico sólo de la Etnomatemática y ese no es nuestro objetivo por ahora.
Desde nuestra visión "Etnomatemática no es Matemática, es la matemática del pueblo como el conjunto de conocimientos matemáticos, prácticos y teóricos, producidos o asimilados y vigentes en su respectivo contexto sociocultural, que supone los procesos de: contar, clasificar, ordenar, calcular, medir, organizar el espacio y el tiempo, estimar e inferir."
Etnomatemática es el camino para aprender Matemática" como el conjunto de los conocimientos matemáticos de la comunidad del aprendiz, relacionados con su cosmovisión e historia, fundamentalmente comprende:
- El sistema de numeración propio.
- Las formas geométricas que se usan en la comunidad.
- Unidades o sistemas de medida utilizadas local o regionalmente (tiempo, capacidad, longitud, superficie, volumen).
- Instrumentos y técnicas de cálculo, medición y estimación; procedimientos de inferencia; otros conceptos, técnicas e instrumentos matemáticos usuales.
- Las expresiones lingüísticas y simbólicas correspondientes a los conceptos, técnicas, e instrumentos matemáticos."[4]
I. ¿QUÉ ES LA ETHNOGEOMETRÍA?
"... Al tratar de transmitir la importancia de las ideas, nosotros las elaboramos con nuestras expresiones occidentales que tenemos de ellas. Desde el principio nosotros diferenciamos, entre las matemáticas que son implícitas y las que son explícitas, y entre los conceptos occidentales que nosotros usamos para describir o explicar y esos conceptos nosotros los atribuimos a la gente de otras Culturas." Marcia Ascher [5]
Ante la falta de literatura y/o de otros autores que hubieran tocado en forma particular a lo que se nos ha ocurrido llamar “Etnogeometría” y considerando que nuestra idea tiene asidero, tanto implícita como explícitamente. Hemos creído conveniente crear, el concepto semánticamente, con la conjunción de Etno+Etnología+Geometría = Ethnogeometría. Como el "Estudio y conocimiento de la Geometría bajo el aspecto cultural de los pueblos comparando sus afinidades de antropología cultural o social y de los lazos de civilización que los caracteriza"[6].
Además tomamos el sentido semiológico del concepto. Porque los códigos que encierra la composición del nombre, se refieren al pueblo, a la gente de nuestros días, a nosotros ahora, por tanto se hace una práctica diaria de la aplicación geométrica en casi todos sus quehaceres.
Para aclarar aun más. Diremos que, cuando se da mayor importancia al aspecto biológico y natural aunado con el psíquico sociológico, etc., estos estudios caen dentro de la Antropología. Mas, si se comprenden en ellos, todos los fenómenos histórico-culturales, además de los puramente naturales, se entra en la Etnología. Ampliando y flexibilizando nuestra visión. Por ejemplo, Etnología vendría a ser, cada reunión de los ICME[7], donde nos congregamos centenares de personas de diferentes razas y nacionalidades que nos sentimos afines por la Matemática o su enseñanza, lo que en otras palabras es estudiar nuestra riqueza material y espiritual con respecto de la Matemática. Mas, sin pretender reuniones tan numerosas tenemos, las de cada día en nuestras comunidades y centros educativos, a los que asisten alumnos de diferentes etnias, pero con un fin común adquirir conocimientos. Esto implica que el mundo actual tiende a hermanar a los hombres de y en todos los confines de la Tierra, y está lejano el día en que se discutió en las universidades de Europa, el problema de sí los negros de Africa o los indios del Nuevo Mundo tenían alma y si eran realmente hombres.
Mientras en la Etnomatemática, los etnomatemáticos intentan describir el mundo matemático, como los otros lo ven. Ethnogeometría, no es el intento de describir, cómo, las ideas se ven a través de los otros. Muy al contrario. Fue y es la generadora no sólo de ideas que todos - etnomatemáticos o no - ven. Tiene una inmanencia permanente[8]. Es el material que inspira a la Etnomatemática, estudiar la historia a partir de la Geometría sea esta euclidiana o no-ecludiana.
La Etnogeometría da lugar a que "... la Etnomatemática...", pueda crear "... un puente entre la Matemática y las ideas (conceptos y prácticas) de otras Culturas." La universalidad de determinadas formas básicas que son parte de una Cultura también universal. Realizar, un estudio etnogeométrico podría ser de mucho mayor interés a los etnomatemáticos, porque partirían de realidades tangibles para luego realizar abstracciones (formular conceptos, o crear teoremas p.ej. sobre equicomposición de poliedros, al observar, los muros de las ruinas incaicas) con una nueva perspectiva. Tal estudio permitiría la posibilidad de matematizar los conceptos o prácticas dentro de una Cultura y, compararla con la otra Cultura, p.ej. que tienen de semejantes la forma de las viviendas de los Uruchipayas del Departamento de Oruro en Bolivia, con la de los africanos de Mozambique; quizá a primera vista diremos la forma cónica de los techos y el material que los cubre.
A partir de la Etnogeometría, el etnomatemático esta obligado a elucidar o aclarar no sólo los conceptos resultantes de las prácticas etnogeométricas, sino, a tomarlos como su material de trabajo para hacer que la Etnomatemática sea el nexo real con la Matemática, porque (como ya lo dijimos), la Etnogeometría, no sólo tiene fundamentos etnológicos, socio-antropológicos, más también, socio-culturales, que han sido y pueden seguir siendo aplicados, al aprendizaje de la Geometría, luego, a la práctica de la Etnomatemática y finalmente a la Matemática..
Por otro lado tomemos lo que dice Marcia Ascher. Que, las cosas las vemos con nuestros ojos occidentalizados, o sea que estamos condicionados a ver siempre bajo esa óptica y cuando alguien lo ve desde otra, nos llama la atención y parece ser incoherente. Eso es comprensible, pues, tantos siglos de academicismo nos han subyugado, que no le damos campo a nuestra mente para pensar de otro modo, sin los símbolos numéricos que representan abstracciones( eso no implica que prescindamos de ellos). Y posiblemente esa sea la razón por la cual hayan aparecido detractores de la Etnomatemática, sin intentar comprenderla, como la nueva aurora para aprender y enseñar a la Matemática.
La Ethnogeometría es parte intrínseca de la vivencia diaria del hombre y su entorno natural[9], pues donde quiera que dirija su atención, a las ruinas de la civilización antigua Inca, "La Puerta del Sol"; las edificaciones de las urbes citadinas (arquitectura) como, la ciudad de Sucre -Bolivia- o, Lima - Perú -, con influencia, de otra cultura, sea francesa, hispana, etc., etc. Antes que Etnomatemática o Matemática. Verá Ethnogeometría y sólo después, Geometría y Matemática; lo mismo será, cuando perciba que una persona es diferente de otra por sus formas anatómicas, complexión física, estatura o color, además su vestimenta, distinta y variada de acuerdo al lugar geográfico en el que habite, con diseños tejidos o estampados en su mayor parte realizados con moldes de hojas, pétalos o tallados matriciales en madera, así como, otras representaciones bordadas en bajorrelieve con una policromía que muestra la riqueza espiritual de los artesanos[10]. Aleatoriamente comparemos los kimonos de los campesinos japoneses, con la túnica o el sari de los hindúes. Las polleras de la chola de las ciudades andinas, que tienen forma arrepollada con la forma de cono truncado de la minifalda de las jóvenes citadinas. En la Naturaleza misma se encuentra con expresiones geométricas (nosotros personas), vemos flores de formas poligonales hojas cardiodes que inspiran coordenadas polares o helechos que generan fractales que luego son colocadas en losdiseños de las vestimentas, casas, etc.. En fin una riqueza espiritual y cultural (inclusive, ideológica por su aplicación),[11] que nos hace admirar. En todas esas expresiones, no vemos ni percibimos inmediatamente ideas, símbolos ni conceptos matemáticos. Estas y éstos se presentarán después, mediante las abstracciones mentales que realicen, los interesados (matemáticos o estudiosos), es decir, se hará Etnomatemática y luego Matemática, partiendo de la Ethnogeometría.
Tenemos otros ejemplos, en los que, “forma, medida y cantidad” están en una simbiosis a primera vista inseparable. Tal el caso de la actividad comercial de los mercados, en los que, las vendedoras colocan sus productos formando montoncitos semejantes a ortoedros, pirámides truncadas o conos, donde. 2 montones (pirámides) de papa por 5 Bs, cuatro montoncitos (conos) de arvejas por 10 Bs. Las vendedoras del mercado pensarían primero en medidas académicas? Sólo, después de que toman conciencia de la forma del cuerpo y de otros aspectos singulares pueden realizar conclusiones de tipo cualitativo y cuantitativo referidas a medir, pesar, contar, comparar y calcular – si, es que, a estas actividades se les puede llamar Matemática. La vendedora del mercado cuando está formando sus “montoncitos” crea las formas que serán más atrayentes al posible comprador (etnogeometriza –si vale el término-), luego determina el valor que tendrá en la venta el montoncito, a montoncitos más grandes con mayor número de unidades (papas, arvejas, frutas, etc.), menos ganancia y, a montoncitos más pequeños menos unidades implica más ganancia según sus costos, dicho de otro modo hace Etnomatemática. No se detiene a pensar si está aplicando un conocimiento académico curricular de Razones y Proporciones o de Reparto Proporcional. Estos, son ejemplos reales y actuales.
Y. ¿Qué podemos decir de los hombres primitivos, que aun no conocían la simbología numeral, cuando trazaron sus pinturas rupestres, luego cuando se hicieron sedentarios y comenzaron a tener noción del derecho de propiedad y el academicismo no había nacido aun? Sin tomar en cuenta, el tiempo, pero, la semejanza entre dos culturas.¿De dónde obtuvieron los Quichuas, el concepto de "Pachatupuy" (Geometría) cuya traducción literal es, Pacha = Tierra y, Tupuy = Medida? La tomarían de los egipcios? Pues, sabemos que ellos dan origen al nombre de "geometría" como resultado de su trabajo anual empírico, al parcelar o reparcelar las tierras aledañas al Nilo después de cada riada. Y como lo leímos, nos admira, toda esa maravilla construida con unos conocimientos básicos de Geometría y de Arquitectura y además con una unidad de medida arbitraria, como era el "codo del arquitecto". A priori podemos afirmar que, la concepción de las formas les obliga (sin ser totalmente empíricos), a crear ciertas unidades de medida y realizar operaciones en ese trabajo y no lo hacen partiendo de hipótesis. Parten de lo que está en su entorno. Utilizan ese conocimiento y el que está, en ellos y con ellos mismos o sea la Ethnogeometría. Parecería que no teorizaron diciendo: "si la base es de n codos entonces la cúspide estará a n codos de altura". Dado que la pirámide para los egipcios no sólo es una tumba para el Faraón. Es la "luz que ilumina el camino", posiblemente dependiendo a qué Faraón iba destinada la pirámide, sería más alta y con menos o más galerías
En otras palabras el ver formas y reproducir formas, está, en él y con el hombre, sin importar la época en la que vive. Por esta observación llamamos parte intrínseca de la vida del hombre. Quizá haya otras maneras de explicarlo mejor y con otras palabras, luego, creemos que, es aquí donde la crítica ayudará a mejorar o retirar esta concepción nuestra proposición. Luego, desde el punto de vista etnogeométrico. Toda percepción, sea ésta real o de abstracción, es global. ¿Quién podría pensar, en la primera contemplación, en conceptos, reglas o axiomas matemáticos al visitar las pirámides Mayas; al contemplar desde el aire, las figuras petroglíficas del Valle de Nazca en el Perú? o las figuras zoomorfas de la Puerta del Sol en Tiwanaku?. ¿Quién piensa primero en las dimensiones o calcula cantidad de material, su valor, o el tiempo que tomará construir algún objeto? Por consiguiente no es Matemática ni Geometría pura lo que manipula el hombre en su diario vivir, al contemplar la belleza de la naturaleza. Es Ethnogeometría como una primera fase. Sin embargo (insistimos), no se queda con ese saber, aplica ese conocimiento y, hace Etnomatemática y finalmente Matemática.
EL TEOREMA MATEMÁTICO DE LA PUERTA DEL SOL
Al lado tenemos, una fracción de “La Puerta del Sol” en Tiwanaku. Y, luego la solución del teorema, presentado por Xavier Amaru Ruiz[12]. Este es, el mejor ejemplo de lo que hasta ahora hemos estado preconizando, de que primero observamos las formas geométricas luego hacemos la matematización.
Y Amaru Ruiz nos dice: “Realizando un análisis lógico a los símbolos e ideogramas grabados en La Puerta del Sol y concentrándonos en el detalle de la aureola que rodea la cabeza del personaje central, notamos, que su planteamiento es sumamente interesante, porque demuestra ser un teorema lógico matemático, en el cual los números y figuras geométricas aparecen virtualmente de manera subliminal, ya que la aureola está rodeada de 18 pares de ganchos (triángulos) rotando en dos direcciones opuestas (18 hacia la derecha y18 a la izquierda) y ambos convergiendo hacia el centro del cuadro, con una constante numeral de 36 (18+18).”
Sin proponérselo Xavier Amaru, hace Etnogeomnetría y Etnomatemática, pues, para el análisis del diseño, ha recurrido a la observación de la forma, “números y figuras geométricas”, pero, va más allá y, él indica: “La figura geométrica de la unificación[13] es el cuadrado, cuya división geométrica da paso a la creación del rectángulo, el triángulo y el círculo. Para tener una constante de 36, sus lados son de valor 6. El área es igual a 36.” “Esta es una matriz simétrica numeral en la cual interaccionan números reales y virtuales, cuyo resultado es una ecuación”.Fig 2.
Al sumar consecutivamente los ocho elementos que constituyen el cuadrado: 1+2+3+4+5+6+7+8 = 36. Si se divide en dos rectángulos verticales, o sea en: “Hemisferio Izquierdo” (HI), sumando 3+4+5+6 = 18; en el “Hemisferio Derecho” (HD), también se tiene 1+2+7+8 = 18
Con dos medianas y dos diagonales ha dividido en triángulos y que partiendo en forma irradiada desde el punto de intersección a la periferia resultan 8, siendo cada uno de 45°, luego 8 x 45° = 360°. La medida del círculo perfecto. Si sumamos verticalmente cada par de los valores asignados a los triángulos: 1+8, 2+7, 3+6, 4+5. El resultado siempre es 9. También da 9 la suma de las cifras significativas de 36 y 360. Y, si borramos todos los triángulos, sólo quedaría la aureola, luego tendríamos un vacío representado por el 0. En consecuencia hemos encontrado dos números virtuales.
La aproximación del valor del Pi andino o Pi matemático
Para encontrar una aproximación al valor de “pi”. El cuadrado mágico se ha dividido en dos partes, mediante una diagonal, tal como, lo muestran las figuras 3 y 4. Cada parte equivale a P/2 (medio “pi”), luego se han realizado estas operaciones: fig. 3.- 4+5+6+7=22, se divide entre 8+1+2+3=14, o sea 22/14=1.571428 y fig. 4, 1+8+7+6=22, se divide 2+3+4+5=14, (1.571428). Si sumamos estos dos cocientes 1.571428+1.571428= 3.142856. Obtenemos el “Pi” andino o matemático con apenas 0.001256 de variación, a la aproximación geométrica de la relación constante entre el diámetro de una circunferencia y su longitud de 3,1416, que encontraron los griegos.
SIMBOLOS NUMERALES
El trazado de los ocho triángulos dentro del cuadrado mágico, no sólo sirve para determinar: el cuadrado, triángulo, rectángulo, circunferencia o la aproximación de “pi”. Es una matriz simétrica para otros aspectos matemáticos entre los que tomamos a los símbolos numerales.
Al observar el gráfico podemos notar que:
Todos los numerales tienen la misma matriz.
Los numerales originales son de uno a cinco, los que siguen, son una imagen espejo.
Xavier Amaru refrenda nuestra observación indicando que: “al juntar los cinco numerales en un bloque se forma dicho cuadrado”. “...y es por este motivo que al sistema numeral tiawanakota se lo consideraba quinario, pero al desdoblarse, los cinco en imagen espejo se conforma la otra mitad”. Por tanto los numerales son 1,2,3,4,5,6,7,8 (reales), 0 y 9 (virtuales). Siendo Y según el mismo autor, una situación parecida de imagen espejo, se da en el sistema arábigo, por ej. Con los numerales 2 y 5; 6 y 9. Ambas observaciones nos llevan a colegir que existe una dualidad simétrica.
Conclusión
Parangonando con la proposición del Prof. Ubiratan D’Ambrosio, diremos que dentro de la Educación, la Matemática es parte de la Etnomatemática y Etnogeometría.
Para finalizar queremos manifestar que, quizá deberíamos haber puesto énfasis, sólo en esta última parte, como la prueba irrefutable de que para ver la Etnomatemática a profundidad, no se puede ignorar a la Etnogeometría como un primer paso. Es decir, partir del valor cultural que tienen las formas geométricas, para luego ir al valor cultural de la matematización. Sin embargo como la vida continua y ella, está ligada a los problemas no sólo socio-culturales, sino, a los socio-económicos, no podemos quedarnos en el pasado, cuando la realidad del “sistema” nos golpea inmisericordemente.
BIBLIOGRAFIA
Asher, Marcia and Robert. : Mathematics of the Incas. Dover Publications Inc. New York 1981
Barton, Bill.: "Teniendo el Sentido de la Etnomatemática: La Ethnomatemática tiene Sentido". The University of Auckland. New Zealand. 1997
Gerdes, Paul: Lusona: Recreações Geométricas de Africa Divisao. Grafica. Da Universidade Eduardo Mondlane. Maputo 1990
Marastroni, G.: Hagamos Geometría. Ed. Fontanela 1980
Pacheco R.,: Un intento de Filosofia de la Matemática. Ed. CEPDI S.C.-Bolivia- 1999
Perero, Mariano: Historia e Historias de Matemática Grupo Editorial Iberoamérica México. 1994
Piaget, Jean:Seis Estudios de Psicología Ed. Seix Barral 1964.
Santaló, L. A.: Geometría No-Euclidiana. Eudeba Buenos Aires Argentina 1985.
Smogorzhevski, A.S. :Acerca de la Geometría de Lobachevski. Ed. Mir Moscú 1984
Ubitan D’Ambrosio Educação Matemática em Revista Número 1, 1993 y otros anexos de la UVLA.
Wyllie, C. R. Jr.: Foundations Geometry. McGraw-Hill New York. 1985
[1] Autor de este capítulo, el cual hemos traducido del original en inglés "Making Sense of Ethnomathematics" Quien a su vez cita: a Marcia Asher, Ubiratan D'Ambrosio y Paulus Gerdes
[2] D'Ambrosio citado por Eduardo Sebastiani Ferreira en “Etnomatemática. Una propuesta Metodológica 1997
[3] Explicación que la dio, en una de las lecciones de la Universidad Virtual Latinoamericana UVLA
[4] Nuevos programas de estudio - Min. Desarrollo Humano Stría. Nal. de Educación 1995
[5] Citada por Bill Barton en su trabajo “Teniendo sentido sobre Etnomatemática: La Etnomatemática tiene sentido”
[6] Hemos armado esta definición partiendo del significado de Ethnos, Etnología y Geometría que se encuentra en los diccionarios enciclopédicos.
[7] Siglas en inglés: Conferencia Internacional de Educación Matemática.
[8] Fuerza o virtud, permanente
[9] D’Ambrosio la definir Etnomatemátiva nos habla del entorno natural y cultural = Etno
[10] La vestimenta de la “Morenada” o la “Diablada” en el carnaval de Oruro –Bolivia-
[11] Porqué se construiría la Gran Muralla China o, el “Muro de Berlín?
[12] Autor de “La Teoría de la Unificación en 20 Dimensiones” 1996
[13] Se refiere a que la teoría del universo se puede desarrallorar completamente con un cuadrado y ocho números.
 La definición de «meme» fue acuñada por el zoólogo, etólogo, teórico evolutivo y divulgador científico Richard Dawkins en las últimas páginas de su libro de 1976 El gen egoísta. Dawkins es un humanista y un escéptico que actualmente está considerado como uno de los intelectuales públicos contemporáneos más influyentes en lengua inglesa; también es conocido como el «rottweiler de Darwin» por sus posicionamientos evolucionistas.
La definición de «meme» fue acuñada por el zoólogo, etólogo, teórico evolutivo y divulgador científico Richard Dawkins en las últimas páginas de su libro de 1976 El gen egoísta. Dawkins es un humanista y un escéptico que actualmente está considerado como uno de los intelectuales públicos contemporáneos más influyentes en lengua inglesa; también es conocido como el «rottweiler de Darwin» por sus posicionamientos evolucionistas.
En aquel momento, sin embargo, Dawkins no era especialmente popular, y su intención tampoco era construir toda una teoría de la cultura bajo aquella palabra inventada, pero un número nada despreciable de científicos y filósofos no pudieron evitar contagiarse de aquella idea tan atractiva y, en lo sucesivo, empezaron a desarrollarla hasta límites que incluso asombraron al propio Dawkins.
De hecho, el propio término «meme» se ha convertido en sí mismo en un meme de gran poder, sobre todo en el ámbito de Internet, donde ha adoptado la definición de cualquier moda o tendencia que se propague rápidamente entre los usuarios. También define a muchas campañas de promoción viral o marketing viral.
Con todo, el término no se unió a la lista oficial de términos a considerar en futuras ediciones del Oxford English Dictionary hasta 1988; una fecha a todas luces muy reciente. Actualmente, la definición que podemos leer en él es: «elemento de una cultura que puede considerarse transmitida por medios no genéticos, especialmente por imitación.»
Y es que la imitación quizá sea el rasgo más humano que existe, y también el rasgo más pertinaz. Todos nacemos con la habilidad innata de imitar lo que nos rodea, porque imitar es una habilidad importante para sobrevivir en un mundo desconocido. Puedes comprobarlo incluso en un bebé: ponte frente a él y ejecuta alguna acción sencilla, como sacar la lengua o emitir gorgoritos. Lo que generalmente sucederá es que el bebé hará lo mismo. Y si le sonreímos, el bebé nos devolverá la sonrisa. De algún modo, hemos transmitido algo al bebé, a pesar de que no entiende nuestro idioma y apenas conoce nada sobre el mundo que le rodea.
Porque cuando imitas a alguien, ese alguien te transfiere parte de lo que posee. Hay muchas palabras distintas para señalar lo que te transfiere específicamente: información, instrucciones, conducta, ideas, etc. Pero todo ello puede designarse con un único término: meme. Un término que en absoluto es gratuito, aunque fue forjado con una pizca de visión de marketing. Tal y como señala el propio Dawkins en El gen egoísta:
Necesitamos un nombre para el nuevo replicador, un sustantivo que conlleve la idea de unidad de transmisión cultural, o una unidad de imitación. «Mímeme» se deriva de una apropiada raíz griega, pero deseo un monosílabo que suene algo parecido a «gen». Espero que mis antiguos clasicistas me perdonen si abrevio mímeme y lo dejo en meme. Si sirve de algún consuelo, cabe pensar, como otra alternativa, que se relaciona con «memoria» o con la palabra francesa même.
La similitud con la palabra gen es importante, porque los memes guardan muchas similitudes con los genes, como recalca Dawkins en su obra:
Al igual que los genes se propagan en un acervo génico al saltar de un cuerpo a otro mediante los espermatozoides o los óvulos, así los memes se propagan en el acervo de memes al saltar de un cerebro a otro mediante un proceso que, considerado en su sentido más amplio, puede llamarse de imitación.

Como adelantábamos en la anterior entrega de este monográfico sobre memética, vamos a profundizar un poco en lo que son los memes. Y también en lo que no son.
Los memes también tienen antecedentes filosóficos, como las ideas de Platón, la filosofía del espíritu deHegel, las distinciones entre noesis y noema de Husserl, la teoría de la ideología de Marx o, en mayor medida, la teoría de los tres mundos de Popper y su defensa de un conocimiento objetivo sin sujeto cognoscente. Memes todos ellos que probablemente también prepararon la mente de Richard Dawkins para pensar en los memes.
Pero ¿cuántas cosas pueden llegar a ser memes? ¿Absolutamente todo lo que nos rodea son memes?
Susan Blackmore es catedrática de Psicología en la Universidad West of England, en Bristol. En la muchas fotografías y conferencias, Blackmore exhibe un aspecto que no tiene mucho que ver con el de una catedrática: su pelo tiene pinceladas de varios colores, como una especie de arco iris capilar. Debido a una complicada enfermedad, Blackmore se vio obligada a permanecer en cama durante mucho tiempo. La mayoría de ese tiempo lo empleó en leer y reflexionar, y una de sus lecturas fue el libro de Richard Dawkins, que la obligó a ir un poco más allá en las implicaciones filosóficas de los memes. Finalmente vertió todas sus conclusiones en su libro La máquina de los memes.
Blackmore sostiene, al igual que Dawkins, que los memes son todo lo que se transmite de una persona a otra mediante la imitación:
ello incluye el vocabulario que utilizamos, las historias que conocemos, las habilidades que hemos adquirido gracias a otros y los juegos que preferimos. También hay que tener en cuenta las canciones que cantamos y las leyes que acatamos. Por lo tanto, cuando conducimos un coche por la izquierda (o por la derecha), tomamos cerveza con curry hindú o coca-cola con pizza, cuando silbamos el estribillo de un «culebrón» televisivo o estrechamos la mano a alguien, estamos tratando con memes.
Los memes se esparcen sin hacer ninguna clase de discriminación. No importa su beneficio o su perjuicio intrínseco. De hecho, pueden ser estéticamente horripilantes, como la canción del verano: un día le pareció pegadiza o agradable a un determinado número de personas, pero ahora, aunque se nos haya atragantado, basta que oigamos las primeras notas para que ya no podamos evitar tararearla. Literalmente, estamos contaminados por ella para el resto de nuestra vida.
 Y es que los memes sólo se basan en su capacidad para replicarse. Es lo único que les concierne. Replicarse sin descanso, cuanto más, mejor. A nosotros de poco o nada nos sirve pasarnos el día entero recordando alguna frase promocional de un producto, pero a los memes les presta un gran servicio.
Y es que los memes sólo se basan en su capacidad para replicarse. Es lo único que les concierne. Replicarse sin descanso, cuanto más, mejor. A nosotros de poco o nada nos sirve pasarnos el día entero recordando alguna frase promocional de un producto, pero a los memes les presta un gran servicio.
Los mecanismos imitativos de la mente son un caldo de cultivo excelente para copiar tonadas. Si una de ellas consigue ser tan popular como para que se incruste en un cerebro y posteriormente transmitirse a otro, lo hará. Si resulta ser extremadamente popular, cantable, recordable, silbable, tiene muchas probabilidades de transmitirse a muchos cerebros. (…) Todo este cantar no tiene ninguna ventaja para nosotros ni para nuestros genes. Sentirse perseguido por esas horribles tonadas es, simplemente, una consecuencia inevitable de poseer un cerebro capaz de imitarlas.
Bajo esta premisa, entonces, podemos entender mejor cómo es posible que canciones tan simplonas y estúpidas como las que se popularizan en verano (y que nos persiguen durante el resto de nuestra vida) tengan una capacidad de contagio tan elevada: sencillamente pueden acceder a más cerebros. Además, las melodías sencillas o repetitivas son más fáciles de recordar. «La música compleja improvisada puede evolucionar aunque es posible que sólo se transmita dentro de un ámbito reducido de músicos expertos o de musicólogos avezados. Es probable que la música realmente sofisticada no sea recordada debido a su complejidad y por lo tanto no se replicará por mucho que produzca placer a sus oyentes.»
Naturalmente, esto es también aplicable a cualquier otra manifestación cultural, como la literatura, los programas de televisión o el cine. Por muy sibaritas o exclusivos que seamos, será prácticamente inevitable que acabemos siendo contagiados por los memes más populares y, a su vez, no podremos evitar también contribuir a la pandemia al transmitirlos a las personas que nos rodean.
Tal vez la prueba más hilarante de esta condición epidémica de los memes sean las últimas palabras pronunciadas por el capitán Berkoz antes de morir. Dieciséis segundos antes de que el vuelo 981 de Turkish Airlines se estrellara contra el suelo, el piloto, el capitán Mejak Berkoz, cantó un jingle publicitario turco, una pegadiza melodía que probablemente había visto en la televisión y que, ni siquiera antes de morir, pudo sacarse de la cabeza.
El divulgador científico Matt Ridley también aporta una divertida anécdota de qué es un meme en su libroGenoma, a través de la relación que mantuvo el antropólogo Lee Cronk con la empresa de calzado deportivo Nike:
Nike hizo un anuncio en la televisión en el que se veía un grupo de personas de una tribu del este de África que levaban botas de montaña. Al final del anuncio uno de los hombres se vuelve hacia la cámara y dice unas palabras. Aparece un subtítulo como traducción en el que pone «Just do it» (hazlo), el eslogan de Nike. Lee Cronk, que habla samburu, el dialecto de los masai, vio el anuncio y fastidió a Nike. Lo que el hombre decía realmente era «no quiero estos zapatos, dame unos más grandes». La mujer de Cronk, periodista, escribió la historia y enseguida apareció en la portada deUSA Today y en el monólogo de Johnny Carson en su programa The Tonight Show. Nike le mandó a Cronk un par de botas grandes; cuando Cronk fue a África otra vez, se las dio a un hombre de la tribu. (…) Pero cuando, unos años después, Internet se expandió, la historia de Cronk encontró un hueco en la Red. A partir de ahí se extendió, sin fecha, como si fuese una historia nueva y Cronk recibe por lo menos una pregunta al mes. La moraleja de la historia es que los memes necesitan un soporte en el que replicarse. La sociedad humana funciona bastante bien; Internet todavía mejor.
 Como adelantábamos en la anterior entrega de este monográfico, los paralelismos entre genes y memes son enormes. Sin embargo, una de las diferencias sustanciales de los genes es que los memes (al menos los buenos memes, con determinado grado de fecundidad, longevidad y fidelidad: por ejemplo, una buena idea, un buen invento, una buena receta de cocina) son capaces de perdurar durante siglos o milenios, como una herencia arqueológica cultural.
Como adelantábamos en la anterior entrega de este monográfico, los paralelismos entre genes y memes son enormes. Sin embargo, una de las diferencias sustanciales de los genes es que los memes (al menos los buenos memes, con determinado grado de fecundidad, longevidad y fidelidad: por ejemplo, una buena idea, un buen invento, una buena receta de cocina) son capaces de perdurar durante siglos o milenios, como una herencia arqueológica cultural.
Porque, si bien el medio de transmisión de los memes puede ser la palabra escrita, la palabra hablada, un gesto, etc., el lugar donde residen los memes es sin duda el paradigma de la seguridad: miles de cerebros diseminados por todo el planeta. Como si realizáramos una copia de seguridad de los archivos más importantes de nuestro disco duro del ordenador en millones de discos duros de los ordenadores de otras personas.
A menudo los genes y los memes se ayudan y se refuerzan entre sí: la cultura no deja de ser, en parte, un reflejo de nuestro ADN (por ejemplo, nos gusta el acto social de comer porque en nuestro genoma está codificada la necesidad de comer y el placer que la comida nos proporcionará, mayormente si contiene cantidades considerables de grasas y azúcares).
Pero esta relación no siempre es tan estrecha. Hay memes que se replican y sobreviven al margen de los genes. Un buen exponente de ello es el meme de la castidad. La castidad, como manifestación genética, no tardaría en desaparecer, porque sencillamente las personas que nacen predispuestas genéticamente a la castidad tendrían menos posibilidades de reproducirse y, por tanto, de transmitir su predisposición a no practicar sexo. No obstante, el meme de la castidad puede tener mucho más éxito, porque una persona casta puede igualmente enseñar a los demás las ventajas morales, sociales o sicológicas de su decisión y, por tanto, contagiarles con el meme de la castidad.
Con todo, una de las propiedades más difíciles de asumir cuando empiezas a entender lo que es un meme es que los memes no tienen entidad física. Un meme no tiene tamaño, ni peso. Tampoco se puede medir, ni observar, ni tampoco catalogar. En ese sentido, un meme es una especie de experimento mental o de metáfora, como la cueva de Platón, el demonio de Descartes, la visión de Hobbes del estado de la naturaleza y el contrato social o la idea de Kant del imperativo categórico. Los memes, pues, están hechos del mismo material del que están hechos los sueños.
Los científicos ni siquiera se ponen de acuerdo sobre lo que es necesario para considerar que algo es un meme y cuándo, en vez de un meme, se trata de un conjunto de memes o de un memeplejo (conjunto de memes que se refuerzan entre sí para crear un meme mayor; por ejemplo, una religión organizada). El filósofoDaniel C. Dennett es probablemente uno de los mayores impulsores de la teoría de la memética, de modo que si queréis profundizar sobre el asunto de los memes, os recomiendo encarecidamente su obra, sobre todo La peligrosa idea de Darwin.
En su obra La peligrosa idea de Darwin, Dennett trata de definir la unidad memética de alguna manera más clara, a fin de que no nos quedemos con la impresión de que los memes son sólo vagos elementos ilusorios. Según Dennet, la unidad memética estaría constituida por el elemento más pequeño que se autorreplica con fecundidad y fiabilidad. Atendiendo a esta definición, Susan Blackmore pone como ejemplo una gota de pintura de un determinado color. Una simple gota de pintura es un meme demasiado pequeño, tan pequeño que no gustará a suficiente número de personas, ni tampoco será objeto de los flashes de las cámaras fotográficas de turistas. Sencillamente, una gota de pintura es algo demasiado común, incluso para Pollock .
Por el contrario, el museo del Louvre o una galería de arte cualquiera constituye un meme demasiado grande. La unidad natural más apropiada sería un cuadro, como por ejemplo El grito de Edgard Munch (sin duda una de las imágenes más empleadas en la cultura popular). Así pues, un meme debe ser lo suficientemente grande como para llevar consigo información que valga la pena copiar; no existe una medida fija para ello:
Los estilos pictóricos, como son el cubismo o el impresionismo, también pueden ser copiados y, por lo tanto, cuentan como memes pero no pueden ser divididos en unidades. Una sola palabra es demasiado corta para otorgarle derechos de autor, pero una biblioteca entera es excesiva para este fin. No obstante, registramos como propiedad intelectual muchas cosas como la apostilla de un anuncio con garra o un libro de cien mil palabras.
Dennett resuelve el problema de que los memes sean entidades de poca precisión comparándolas con las palabras. Para Dennett los memes existen en tanto en cuanto existen las palabras. Por ejemplo, cuando un chico lleva una gorra de béisbol hacia atrás, ¿estamos frente a un meme o frente a dos memes (el de llevar la gorra y el de ponérsela hacia atrás)?. La verdad es que el matiz no es tan problemático como parece, porque este equívoco también se produce en el ámbito del lenguaje y no por ello dudamos de que el lenguaje exista: por ejemplo, ¿la palabra «rompecorazones» es una palabra o son dos?
Tened todo esto en cuenta la próxima vez que una idea se alumbre en el ámbito de vuestro craneo. Probablemente, haya sido alumbrado en otros cráneos, y en el vuestro sencillamente ha germinado.
Como un virus. El virus de la mente.

En demasiadas ocasiones, imponer el bien produce incluso más dolor que hacer el mal. Eso sucede, por ejemplo, porque no siempre conocemos los efectos secundarios que producirá nuestra buena fe.
En otras ocasiones, producir un daño es la única manera de producir un bien mayor (imaginemos que queremos que la gente pueda estacionar su coche en el centro de una ciudad: a priori todos querremos que el aparcamiento fuera gratuito, pero ello solo provocaría grandes atascos y la seguridad de que nunca encontraremos sitio libre. La única forma de estacionar en el centro de una ciudad es imponiendo un pago por estacionar; una lógica que también se aplica a no construir más carreteras: cuantas más aparecen, el tráfico se incrementa, , así que se debe “fastidiar” al conductor con algunos atascos para que se lo piense mejor la próxima vez que quiera usar su coche).
Si nos ponemos a dilucidar los derechos de los ciudadanos en relación a su etnia, su sexo, su religión y demás factores, entonces las buenas y malas acciones todavía se enredan más, confundiéndose unas con otras. A fin de que, entre todos, podamos profundizar un poco más en nuestras ideas al respecto, hoy vamos a tratar un tema ciertamente peliagudo: ¿hombres y mujeres deberían percibir el mismo salario a fin de combatir las desigualdades laborales en relación al sexo?
Dejemos de lado por un rato nuestras ideas preconcebidas y vayamos al meollo.
Lo primero que deberíamos aclarar es si las mujeres SIEMPRE reciben un salario menor debido a su sexo y no a otras razones. En principio, si un hombre y una mujer hacen el mismo trabajo (con el mismo nivel de antigüedad, el mismo nivel de entrenamiento, etc.) deberían percibir el mismo salario (y lo mismo debería suceder en el caso de dos hombres o dos mujeres, aunque también se produzcan injusticias al respecto… lo cual debería hacernos sospechar que, tal vez, no todas las desigualdades salariales respondan a una discriminación sexual).
El problema es que hay algunos sectores laborales dominados casi totalmente por las mujeres, así que no hay hombres en estos sectores que sirvan como clase comparativa, con lo que es difícil aseverar si el bajo salario de una mujer en este contexto se debe necesariamente a una discriminación sexual. Para soslayar esto, se ha aceptado la afirmación discutible de que hombres y mujeres deben recibir igual salario por un trabajo de igual valor (entendiéndose “valor” como la conjunción de cuatro factores básicos: habilidad, esfuerzo, responsabilidad y condiciones de trabajo). A esto se le llama en Estados Unidos “valor comparable”, y en Canadá, “equiparación salarial”.

Si echamos un vistazo a las tablas comparativas de un informe de la Comisión de Derechos Humanos Canadiense, por ejemplo, descubriremos que el trabajo de recepcionista recibía un valor por puntos de 320, el mismo que el trabajador de un almacén. Sin embargo, el recepcionista tenía un sueldo anual de 28.000 dólares, y el trabajador de almacén de 33.000 dólares. Hemos de sospechar, entonces, que algo funciona mal. Quizá es que se está valorando más un trabajo masculino y físico como trabajador de almacén que un trabajo más femenino como recepcionista.
Sin embargo, este razonamiento tiene un punto débil. ¿Por qué las mujeres escogen un trabajo peor pagado cuando podrían ganar más siendo trabajadoras de almacén? La respuesta que enseguida viene a la mente es del tipo “es más difícil que el mercado laboral acoja a una mujer como trabajadora de almacén por pura discriminación de género”. Pero tal y como señala el filósofo Joseph Heath en su libro Lucro sucio:
Pero si ésta es la explicación, la forma correcta de combatir el diferencial salarial sería asegurar que las mujeres tengan igual acceso a tales ocupaciones, eliminar la discriminación a la hora de contratar. La manera más fácil de eliminar los guetos es facilitar que la gente salga de ellos. Pero, desde luego, es dudoso que muchas recepcionistas se interesen por trabajar en los almacenes. Una razón es que la gente tiene diferentes tipos de habilidades y gustos, y tiende a buscar un trabajo lo menos pesado posible, dadas sus preferencias. Los trabajadores del almacén y las recepcionistas no salen de las mismas bolsas de trabajo; las vacantes en un área no se llenarán de solicitantes de la otra. Puede haber una docena de solicitantes para cada trabajo vacante como recepcionista, y sólo dos o tres para trabajos en el almacén. Los trabajadores de almacén acaban siendo mejor pagados simplemente porque están en un mercado de trabajo menos competitivo.
Obviamente, la psicología social y la sociología son ciencias muy blandas y deben controlar muchas variables que aún quedan lejos de sus competencias, así que en ningún momento se afirma aquí que lo que sucede realmente en el mundo es lo que expone Josep Heath. Lo que se afirma es que no se puede inferir la presencia de discriminación por el simple hecho de que se retribuya el trabajo de igual dificultad con distintas remuneraciones. Lo que se afirma, en definitiva, es que las cosas no siempre son tan sencillas y básicas como parecen.
Pero lo cierto es que los salarios no solo se establecen en base a la dificultad de un trabajo o la habilidad requerida para llevarlo a cabo, sino también en base a si se requiere más o menos gente para desempeñar el trabajo en cuestión. Precisamente los trabajos esencialmente femeninos adolecen del mismo problema: mucha gente (mujeres) compiten por una oferta limitada de trabajo. Ello devalúa los salarios, independientemente de si existe discriminación por género o no.
De nuevo, si ésa es la situación, entonces no estamos tratando el problema con los mecanismos adecuados:
Desde luego, la limitación de las opciones de carreras profesionales que han tenido históricamente las mujeres es el legado de una discriminación en otros sectores. Las mujeres han hecho tradicionalmente ciertos tipos de trabajo porque se les negaban otras opciones. La solución, en cualquier caso, no es incrementar los salarios del sector femenino: precisamente, eso envía la señal equivocada. Se debe desincentivar a las mujeres a buscar trabajo en campos sobresaturados, no retribuirlas con salarios mayores. Los empleadores a gran escala, como el Gobierno, pueden igualar los salarios en algún grado (lo mismo que las universidades pueden pagar en exceso a los profesores de Filosofía), pero los efectos sobre los incentivos a menudo son perversos.

Por ejemplo, si se paga mucho más a los médicos que a las enfermeras, también es porque toda una generación de mujeres que podían haber sido doctoras se vio forzada a trabajar como enfermeras. Los salarios de las enfermeras no ascendió, y las mujeres empezaron a desear convertirse en doctoras para ganar dinero. Hasta el punto de que ahora los hospitales están empezando a sufrir un déficit de enfermeras preparadas.
Ello, irónicamente, está provocando que los salarios de las enfermeras estén creciendo, al tiempo que decrecen los salarios de las médicos (en parte porque las médicos trabajan, de media, menos que los médicos). Como veis, las causas y efectos de cada acto son difíciles de gobernar e incluso de predecir.
Y no toda diferencia entre sexos se debe necesaria y exclusivamente a una discriminación por sexo.
Una vez eliminada la discriminación activa contra las mujeres en las escuelas de Medicina, la desigualdad de pago se elimina sin que haga falta tomar cartas en el asunto e influir en los salarios. Si hace 20 años hubiéramos incrementado artificialmente los salarios de las enfermeras, habría sido negativo para el objetivo más amplio de lograr la igualdad de género, en tanto que habría disminuido el incentivo que tantas mujeres jóvenes tienen para convertirse en doctoras.
Otro asunto que debemos tener en cuenta es si realmente las mujeres tienen las mismas ganas de trabajar y de ganar el máximo dinero posible que los hombres. Si no fuera así, entonces incentivar la igualdad salarial sería en realidad discriminatorio para que los tienen más ambición, pertenezcan al sexo que pertenezcan.
Este espinoso asunto ha sido tratado más ampliamente en el artículo ¿Por qué las mujeres perciben un salario inferior al de los hombres? (I) y (y II).
Recordemos que son estudios que no controlan todas las variables, pero precisamente por ello deberíamos ser cautos a la hora de inclinar la balanza de nuestra opinión hacia un lado u otro, y no dar las cosas siempre por sentado. De ello no se denota que seamos machistas o feministas, sino honrados intelectualmente.
Y ahora del dabate queda abierto.

Ya os comentaba en ¿Por qué el día tiene 24 horas? de dónde venía esa división del tiempo.
En esta ocasión, me gustaría contaros 10 métodos para medir el tiempo.
A través de los siglos, las personas hemos creado algunos métodos bastante curiosos para medir el tiempo, desde los relojes de sol, muy básicos, hasta los relojes atómicos de cesio de hoy día.
Vamos a echar un vistazo a una gran variedad de métodos, unos conocidos, otros no tanto y otros que son tan antiguos como el mismo tiempo.
Como os dije en su momento, los egipcios fueron la primera civilización que aportaron a la ciencia objetos que hacían funciones de reloj. Ellos construyeron los obeliscos alrededor de 3500 A.C. y los colocaron en lugares estratégicos donde se proyectaban sombras. Al principio, estos obeliscos sólo permitían saber cuando era el mediodía, pero más tarde marcó el tiempo en otras subdivisiones.
Pasados los años los egipcios desarrollaron los primeros relojes de sol que funcionaban mediante el seguimiento del Sol.
Una hoja proyecta una sombra que apunta a un número marcado en la cara del reloj de sol, como una especie de reloj con sólo la manecilla de las horas.
Por supuesto, con un reloj solar no se podía saber la hora en un día nublado o de noche. También era inexacto porque el Sol está en ángulos diferentes en las distintas estaciones del año, las horas eran más o menos largas dependiendo de la temporada.
Sin embargo, un reloj de sol era mejor que nada, y allá por el año 30 A.C. estaban en uso más de 30 tipos diferentes en Grecia, Italia y Asia Menor.
Incluso hoy en día, el Sol está en el centro de nuestro sistema de cronometraje, ya que las zonas horarias están establecidas por la rotación de la Tierra con respecto al Sol.
Fueron también los antiguos egipcios los que desarrollaron el primer método de medida del tiempo en la noche. Para ello, inventaron la primera herramienta astronómica, alrededor de 600 A.C., el merjet.
Un merjet es una cadena con un peso en el extremo utilizado para medir una línea recta, al igual que un carpintero hoy día utiliza una plomada.
Los astrónomos egipcios alineaban dos merjets con la estrella Polar y la usaban para marcar una línea norte-sur en el cielo nocturno. El tiempo se contaba conforme ciertas estrellas cruzaban esa línea.
Las estrellas también se pueden utilizar para marcar el paso, no sólo de horas, sino días. Esta medición de la rotación de la Tierra se denomina tiempo sideral.
Cuando cierto punto imaginario entre las estrellas cruza un meridiano se llama medio día sideral. El tiempo transcurrido desde un medio día sideral a otro se le llama día sideral.

Los seres humanos hemos estado midiendo el tiempo durante un período relativamente corto de nuestra historia.
El deseo de sincronizar nuestras actividades llegó hace unos 5.000 o 6.000 años cuando nuestros antepasados nómadas comenzaron a asentarse y construir civilizaciones.
Antes de eso, dividíamos el tiempo en días y noches; días brillantes para la caza y oscuras noches para dormir.
Pero cuando la gente comenzó a sentir la necesidad de coordinar sus acciones, ser puntuales para las reuniones públicas, por ejemplo, necesitaban un sistema unificado para medir el tiempo.
Cualquiera que haya visto El mago de Oz conoce el poder de este reloj. ¿Quién no se asustó cuando la malvada Bruja del Oeste entregó este reloj a Dorothy y le dijo que sólo tenía una hora de vida?
El reloj de arena se remonta siglos. Se compone de dos ampollas de vidrio, una encima de la otra, con una abertura estrecha entre ellas. La arena se extiende desde la parte superior de la bombilla a la parte inferior cuando el reloj se vuelca.
Cuando se vacía el bulbo superior el tiempo se acaba, pero no necesariamente tiene que ser una hora, como hasta ahora todos los relojes. Un reloj de arena podía ser construido para medir casi cualquier período corto de tiempo mediante la alteración del tamaño de la abertura entre los bulbos o cambiando la cantidad de arena en el vaso.
Los relojes de agua, conocidos como clepsidras (del griego “ladrón de agua”), se encontraban entre los primeros dispositivos que no necesitaban el sol o las estrellas para calcular el tiempo, lo que significa que podría ser utilizado en cualquier momento del día.
Los relojes de agua funcionan mediante la medición de agua que gotea de un recipiente a otro. Fueron inventadas en Egipto, pero su uso se extendió en todo el mundo antiguo y hasta bien entrado el siglo XX la gente todavía tenían relojes de agua.
Los antiguos griegos y romanos construyeron impresionantes torres para albergar sus relojes de agua. En China a estos relojes se les llamaba Lou y a menudo eran de bronce.
Sin embargo, a pesar de que los relojes de agua fueron una imposición de estructuras, no eran muy precisos.
A través de los siglos, las personas han desarrollado todo tipo de maquinaria para saber la hora.
Los chinos inventaron el reloj de incienso entre 960 y 1279, y su uso se extendió en todo el este de Asia. Se trataba de un tipo de reloj con unas bolas de metal con una cuerda. Cuando el incienso se consumía, las bolas caían haciendo sonar un gong que anunciaba la hora.
Otro ejemplo son los relojes de vela que numeraban unas marcas. Cuando la vela se quemaba a una marca determinada, el dial anotaba el tiempo. Era muy usado en los monasterios para las vigilias.

Muchos podéis decir que nos estamos engañando a nosotros mismos si realmente pensamos que mantenemos noción del tiempo, si es real o no lo es.
Albert Einstein dijo:
La distinción entre pasado, presente y futuro es sólo una ilusión obstinadamente persistente
Sus paseos más allá de la torre del reloj en Berna, Suiza, le llevaron a algunas ideas que cambiaron la naturaleza del tiempo, cosa que veremos más tarde.
Si el tiempo es real o no, la medición del tiempo se ha convertido en algo vital para nuestras vidas y eso no hay quien lo niegue.
En Europa, durante 1300, las musas de la invención empezaron a hacer los relojes mecánicos que se ejecutaban gracias a un sistema de pesos y muelles. Estos primeros relojes no tenían agujas, sólo una campana que sonaba cada hora en punto.
Estos primeros relojes grandes se instalaron en las iglesias o monasterios para anunciar las oraciones y servicios.
Pronto los relojes con agujas comenzaron a aparecer, y más tarde, una vez que el péndulo se fue refinando, se añadió otra manilla para realizar un seguimiento de los minutos.
El desarrollo de los muelles allanó el camino para la fabricación de relojes de mesa, aunque eran notoriamente inexactos.
En 1714, el Parlamento británico ofreció una recompensa a cualquiera que pudiera diseñar un reloj de precisión para ayudar en la navegación marítima. El reloj ganador eran tan exacto que tenía un error de sólo cinco segundos por cada seis semanas y media.
Pero no fue hasta la Revolución Industrial cuando comenzó la producción masiva de relojes.
El descubrimiento de resortes espirales que permitían mover las manecillas de un reloj hizo posible que un diseño más pequeño fuese posible.
Los relojes de bolsillo estaban a la orden del día en hombres, mientras que los relojes de pulsera eran considerados joyas, aunque sólo para mujeres.
Todas esas reglas de moda cambiaron durante la Primera Guerra Mundial, cuando mirar la hora en un reloj de bolsillo era imposible durante la batalla. Durante el resto del siglo XX, casi todo el mundo, especialmente los hombres, llevaban relojes de pulsera.
Regalar un reloj simboliza el paso a la edad adulta y muchas empresas se prestaban a obsequiar con un reloj de oro en las jubilaciones.
Actualmente el reloj de pulsera va perdiendo estilo y uso. En casa o en el trabajo podemos ver la hora en el ordenador, mientras que si estamos fuera en los teléfonos móviles, etc. ¿Qué será de ellos?

Y para terminar con esta obsesión por el tiempo quería hacerlo con las formas “más modernas” de medirlo. Aunque no todo van a ser relojes…
Cuando el reloj de cuarzo apareció una especie de electricidad comenzó a mover las manillas, dejando atrás los engranajes y pesos.
El cuarzo es piezoeléctrico, lo que significa que cuando un cristal de cuarzo se presiona genera una pequeña corriente de electricidad que hace que el cristal vibre. Todos los cristales de cuarzo vibran en la misma frecuencia.
Los relojes de cuarzo utilizan una batería para crear la vibración del cristal y un circuito para contar las vibraciones. El circuito utiliza esta información para generar un pulso cada segundo. Estos pulsos sirve de energía en los engranajes de un reloj mecánico o de alimentación en la pantalla de un reloj digital.
Los relojes de cuarzo siguen dominando el mercado debido a su precisión y el bajo coste de producción.
Aunque el nombre suena un poco amenazante, los atómicos relojes no son peligrosas en absoluto. Miden el tiempo mediante el seguimiento de cuánto tarda un átomo en cambiar su estado de energía de positivo a negativo y viceversa.
El tiempo estándar oficial de los Estados Unidos se establece por el NIST F-1, el reloj atómico de cesio del Instituto Nacional de Ciencia y Tecnología (NIST) en Boulder, Colorado.
Los científicos introducen el gas de cesio en la cámara de vacío del reloj, a continuación dirigen haces de láser infrarrojo en ángulos de 90 grados hacia el centro de la misma. Los láseres obligan a los átomos, pegados en una bola, a dirigirse a una zona llena de microondas.
Los científicos miden el número de átomos con los estados alterados y ajustan las microondas de distintas frecuencias para que la mayoría de los átomos se alteren. Esta frecuencia final es la frecuencia de resonancia natural para los átomos de cesio y constituye el número de oscilaciones que definen un segundo.
Suena complicado, pero el resultado es un valor estándar para el segundo. Los relojes de todo el mundo pueden configurarse automáticamente del estándar NIST por zona horaria.
El reloj atómico mantiene un registro de tiempo en el nivel más minúsculo.
Como hemos visto, el recuento real de los minutos y los segundos requiere algunos procedimientos complejos y maquinaria, pero el recuento de días y meses se basa en algo que cualquiera puede observar, la posición del sol y la luna. Las diferentes culturas utilizan diferentes métodos.
El calendario gregoriano (o cristiano), el más usado y común hoy en día, se basa en el Sol. El calendario islámico utiliza las fases de la luna. Mientra que los calendario judíos y chinos se basan en una combinación de ambos métodos.
En el calendario gregoriano un día es una rotación completa de la Tierra sobre su eje. Un mes tiene unos 29,5 días, lo cual es un ciclo completo de fases de la luna, y un año es 364.24 días, el tiempo que tarda la Tierra en orbitar alrededor del Sol.
Para regular todo se crearon los años bisiestos, que duran 366 días en vez de los 365 de un año común. Es porque de cada año sobran 6 horas y en 4 años son 24 horas, eso forma un día. Por cierto, ¡Felíz día extra!
Vía | Discovery

La historia de la evolución del hombre siempre estuvo ligada a su curiosidad por conocer lo que lo rodeaba y a su comprensión al respecto. Las “pequeñas luces del cielo” y todos los fenómenos astronómicos relacionados con ellas llamaron la atención de algunos más que de otros, por lo que en pocas líneas intentaremos detallar quienes fueron los astrónomos importantes que hicieron historia.
Tales de Mileto proclamaba 700 años A.C. que la tierra era redonda, que era circundada por una masa grisácea llena de agujeros y que todo era iluminado por una “llama eterna” explicando casi el día y la noche. Anaximandro, Pitágoras, Platón, Aristóteles plantearon 200 años después que la tierra era el centro del universo y que todo giraba a su alrededor formalizándose la concepción de la redondez de la misma, producto de la observación de su sombra proyectada sobre la luna en un eclipse.
Fue Aristarco de Samos quien deduce en sus estudios que la tierra giraba junto con las demás estrellas alrededor del sol. Las observaciones de Eratóstenes, Hiparco de Nicea y Posidonio de Apamea realizadas 100 años A.C. colaboraron con el cálculo de la circunferencia de la tierra, la relación entre las mareas y las fases lunares y la distancia entre los planetas y el sol, que por momentos variaba.
Ptolomeo y su teoría geocéntrica del universo, que coincidía con la postura eclesiástica de la época perpetuó por casi 1400 años esta concepción hasta que Copérnico desarrolló la teoría Heliocéntrica que plantea que todo el universo gira alrededor del sol, incluso la tierra (por supuesto que esta idea encontró mucha oposición en su época).
Ticho Brahe desarrolló mejores instrumentos de medición y observación y basado en sus estudios refutó algunos aspectos de la teoría de Copérnico. Galilei, Kepler, Newton, el mismísimo Einstein, Powell Hubble y Carl Sagan fueron en la modernidad y la actualidad los que aportaron tanto teorías como así los elementos técnicos cuyo fruto es nuestro actual saber sobre este campo del cual aprendemos a pasos vertiginosos cada día.
Algo es seguro, así como sucedió desde un principio, con cada descubrimiento nuestra concepción del universo también evolucionará.
